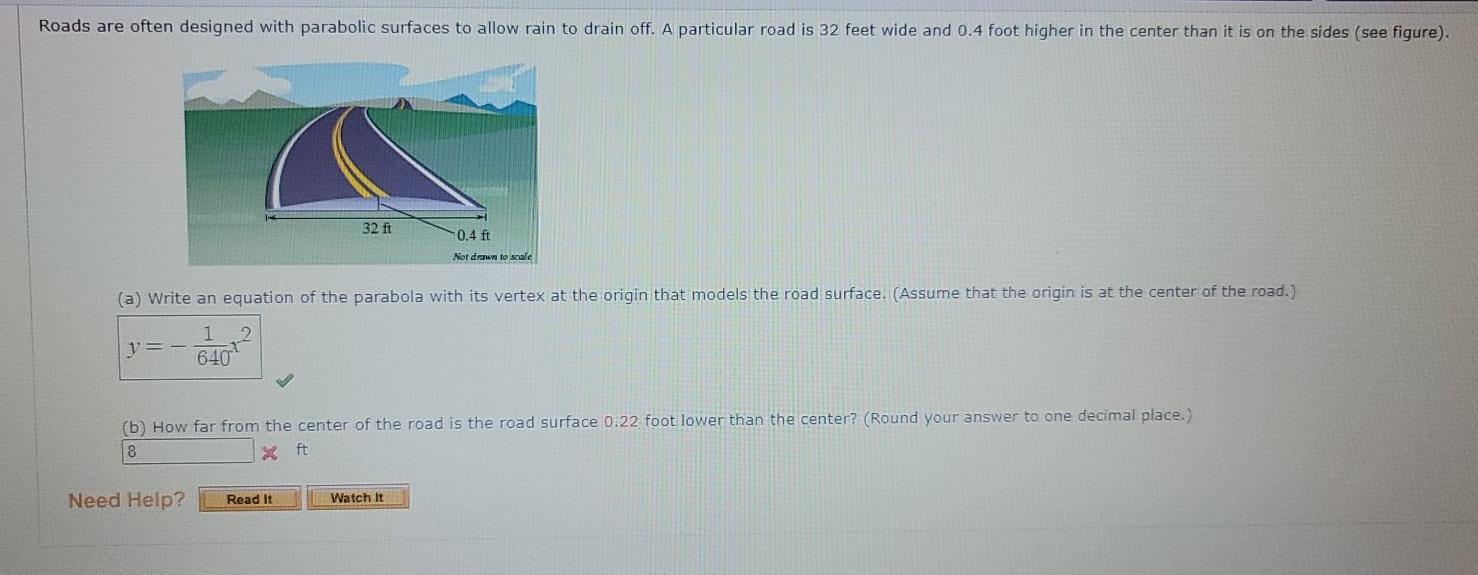
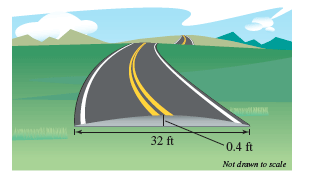
Assume that the origin is at the center of the road. A particular road that is 32 feet wide is 04 foot higher in the center than it is on the sides see figure.
Solved Roads Are Often Designed With Parabolic Surfaces To Chegg Com
A particular road that is 32 feet wide is 04 foot higher in the center than it is on the sides see figure.

. That models the road surface. A road surface in its simplest form consists of a smoothed surface in effect the subgrade. 32 ft 04 ft Nor draw to scale a Write an equation of the parabola with its vertex at.
Suppose a road is 32 feet wide and 04 foot higher in the center than it is on the side. Find the slope and change in elevation over a one-mile section of the road. In order to allow rain to run off of a road they are often designed with parabolic surfaces in mind.
A Find an equation of the parabola that models the road surface. A particular road is 32 feet wide and 04 foot higher in the center than it is on the sides see figure. 1 A straight road rises at an inclination of 03 radian from the horizontal.
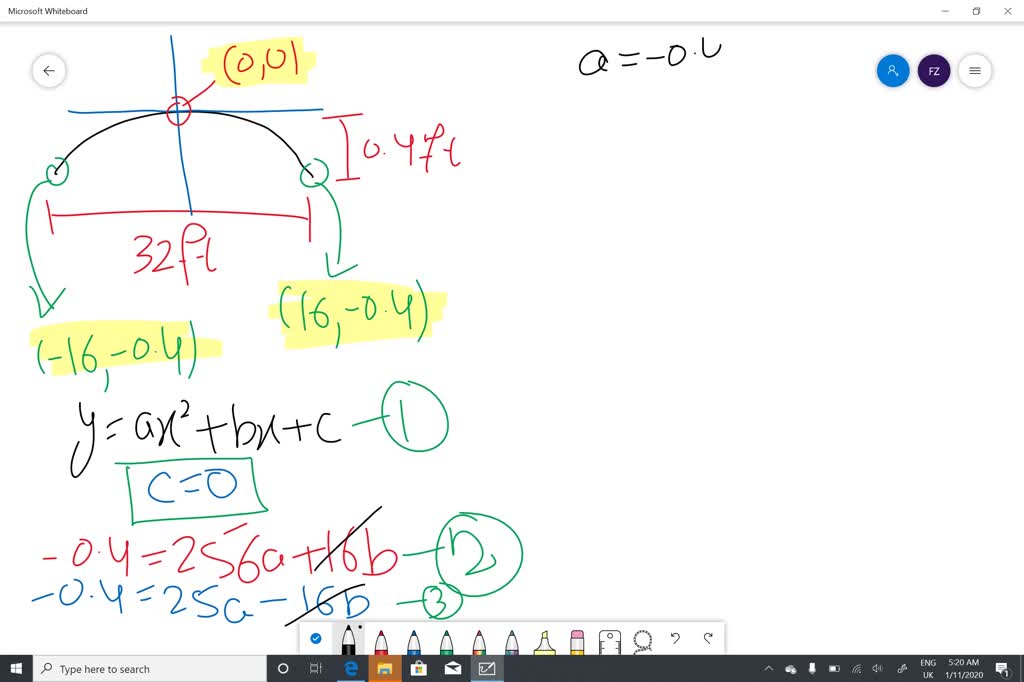
B How far from the center of the road is the road surface 02 feet. Find an equation of the parabola that models the road surface. A Write an equation of the parabola with its vertex at the origin that models the road surface.
A particular road is 32 feet wide is 04 foot highter in the center than it is on the sides Glb-qò a Find an equation if the parabola with its vertex at the origin that models the road surface pc-Ibo b How far from the center of the road is the road surface. A Develop an equation of the parabola with its vertex at the origin. A particular road that is 32 feet wide is 04 foot higher in the center than it is on the sides see figure.
Find the equation of the parabola that models the the road surface by assuming that the center of the parabola is at the origin. A particular road is that is 32 feet wide is 4 feet higher in in the center then on the sides. Roads are often designed with parabolic surfaces to allow rain to drain off.
Find the equation using the form. I am struggling to get an equation of the parabola with its vertex at the origin. Roads are designed with parabolic surfaces to allow rain to drain off.
2 In order to allow rain to run off of a road they are often designed with parabolic surfaces in mind. Assume that the origin is at the center of the road. A particular road that is 32 feet wide is 04 foot higher in the center that it is on the sides.
A particular road that is 32 feet wide is 04 foot higher in the center than it is on the sides see figure. Find an equation of the parabola that models the road surface. Road Design Roads are often designed with parabolic surfaces to allow rain to drain off.
Suppose a road is 32 feet wide and 04 foot higher in the center than it is on the side. That models the road surface. Roads are often designed with parabolic surfaces to allow to drain off.
Assume that the origin is at the center of the road. Assume that the origin is at the center of the road a. Road Design Roads are often designed with parabolic surfaces to allow rain to drain off.
Dirt roads would fall into this category. 2 In order to allow rain to run off of a road they are often designed with parabolic surfaces in mind. Sediment production from dirt road surfaces is high.
Find the slope and change in elevation over a one-mile section of the road. Suppose a road is 32 feet wide and 04 foot higher in the center than it is on the side. Ax2 bx c y.
Roads are often designed with parabolic surfaces to allow rain to drain off. 1 A straight road rises at an inclination of 03 radian from the horizontal. Suppose a road is 32 feet wide and 04 foot higher in the center than it is on the side.
In order to allow rain to run off of a road they are often designed with parabolic surfaces in mind. ROAD DESIGN Roads are often designed with parabolic surfaces to allow rain to drain off. Assume that the origin is at the center of the road.
Cross section of road surface a Find an equation of the parabola that models the road surface. ROAD DESIGN Roads are often designed with parabolic surfaces to allow rain to drain off. Suppose a road is 32 feet wide and 04 foot higher in the center than it is on the side.
A particular road that is 32 feet wide is 04 foot higher in the center than it is on the sides see. Find an equation of the parabola with its vertex at the origin that models the road surface. ROAD DESIGN Roads are often designed with parabolic surfaces to allow rain to drain off.
Roads are often designed with parabolic surfaces to allow rain to drain off. A particular road that is 32 feet wide is 04 foot higher in the center than it is on the sides. Roads are designed with parabolic surfaces to allow rain to drain off.
A particular road is 32 feet wide and 04 foot higher in the center than it is on the sides see figure. Roads are often designed with parabolic surfaces to allow rain to drain off. 1 A straight road rises at an inclination of 03 radian from the horizontal.
2 In order to allow rain to run off of a road they are often designed with parabolic surfaces in mind. Assume that the origin is at the center of the road. A Find an equation if the parabola that models the road surface.
Roads are often designed with parabolic surfaces to allow rain to drain off. And determine How far from the center of the road is the road surface 02 feet. Suppose a road is 32 feet wide and 04 foot higher in the center than it is on the side.
A particular roads 32 feet wide and 04 foot higher in the center than it is on the sides see figure 041 Wine an equation of the parabola with its vertex at the origin that models the road surface Assume that the origin is at the center of the road. A Find an equation of the parabola that models the road surface. That models the road surface.
Obviously dirt roads are only useful where the road is expected to receive intermittent light use and is not affected by climate. A particular road that is 32 feet wide is 04 foot in the center than it is on the sides. Up to 24 cash back b Roads are often designe wi parabolic surfaces to allow for rain to drain off.
Roads are often designed with parabolic surfaces to allow to drain off. In order to allow rain to run off of a road they are often designed with parabolic surfaces in mind. Road Design Roads are often designed with parabolic surfaces to allow rain to drain off.
A Find an equation of the parabola that models the road surface. A particular road that is 32 feet wide is 04 foot higher in the center than it is on the sides. A particular road that is 44 feet wide is 04 foot higher in the center than it is on the sides see figure.
Find the slope and change in elevation over a one-mile section of the road.
Solution Roads Are Designed With Parabolic Surfaces To Allow Rain To Drain Off A Particular Road That Is 32 Quot Feet Wide Is 0 4 Foot Higher In The Center That It Is On

Solved 7 Roads Are Often Designed With Parabolic Surfaces Chegg Com
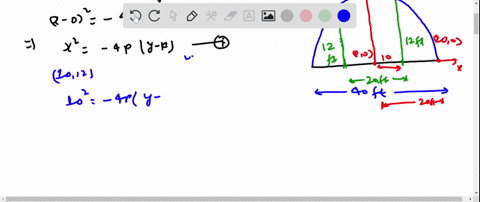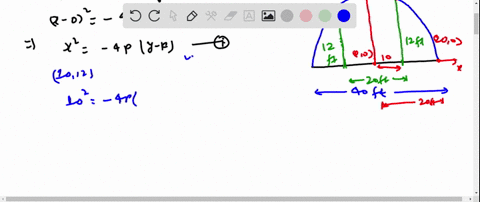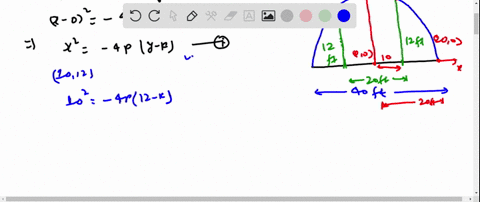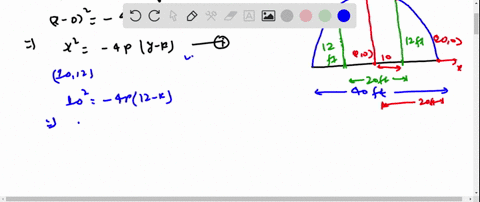
Solved Road Design Roads Are Often Designed With Parabolic Surfaces To Allow Rain To Drain Off A Particular Road That Is 32 Feet Wide Is 0 4 Foot Higher In The Center Than It
Solved Roads Are Often Designed With Parabolic Surfaces To Chegg Com

Solved Roads Are Often Designed With Parabolic Surfaces To Chegg Com

Solved Roads Are Often Designed With Parabolic Surfaces To Allow Rain To Drain Off A Particular Road That Is 32 Feet Wide Is 0 4 Foot Higher In The Center Than It Is On

Solved Roads Are Often Designed With Parabolic Surfaces To Chegg Com
Solved Road Design Roads Are Often Designed With Parabolic Surfaces To Allow Rain To Drain Off A Particular Road That Is 32 Feet Wide Is 0 4 Foot Higher In The Center Than It
0 comments
Post a Comment